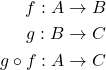Chapter 1
1.1) Implement, as best as you can, the identity function in your favorite language (or the second favorite, if your favorite language happens to be Haskell).
function identity(x) {
return x;
}If we would like to be more type-strict, we could use TS.
function identity<T>(x: T) {
return x;
}1.2) Implement the composition function in your favorite language. It takes two functions as arguments and returns a function that is their composition.
function composition<T1 extends any[], T2, T3>(
f: (p: T2) => T3,
g: (...p: T1) => T2
) {
return function (...p: T1) {
return f(g(...p));
}
}
function add(a: number, b: number) {
return a + b;
}
function mul100(x: number) {
return x * 100;
}
const f = composition(mul100, add);
console.log(f(10, 30)); // prints 40001.3) Write a program that tries to test that your composition function respects identity.
function lIdentity<A extends any[], B> (g: (...x: A) => B){
return function (...x: A) {
return composition(identity, g)(...x);
}
}
function rIdentity<A, B>(f: (x: A) => B) {
return function (x: A) {
return composition(f, identity)(x);
}
}
const f1 = rIdentity(mul100);
const f2 = lIdentity(mul100);
console.log(f1(100) === f2(100)); // true
console.log(f1(0) === f2(0)); // true
console.log(f1(0) !== f2(10)); // true
// ...1.4) Is the world-wide web a category in any sense? Are links morphisms?
No. The transitive property is not always fulfiled.
We can definitely find pages, where:
– Link from page A points to page B.
– Link from page B points to page C.
– There is no link from A to C – thus transitive property is not fulfiled.
1.5) Is Facebook a category, with people as objects and friendships as morphisms?
No. Because of same reason as in 1.4.
1.6) When is a directed graph a category?
When for every directed path {(A,B), (B, C)} (where A, B, C are nodes of graph) exists edge (A, C). And for every node V exists edge (V, V).
2.1) Define a higher-order function (or a function object) memoize in your favorite language. This function takes a pure function f as an argument and returns a function that behaves almost exactly like f, except that it only calls the original function once for every argument, stores the result internally, and subsequently returns this stored result every time it’s called with the same argument. You can tell the memoized function from the original by watching its performance. For instance, try to memoize a function that takes a long time to evaluate. You’ll have to wait for the result the first time you call it, but on subsequent calls, with the same argument, you should get the result immediately.
function memo <A extends any[], B>(f: (...x: A) => B) {
const memory: Record<string, B> = {};
return function(...x: A): B {
const key = JSON.stringify(x);
if(memory[key]) {
return memory[key];
}
memory[key] = f(...x);
return memory[key];
}
}
function getRunTime<A extends any[], B>(f: (...x: A) => B, ...params: A): Number {
const start = new Date().getTime();
f(...params);
const stop = new Date().getTime();
return stop - start;
}
function takeLong(returnValue: Number) {
for(let i = 0; i<1000000000; i++) {}
return returnValue;
}
console.log(getRunTime(takeLong, 1)); // 750
console.log(getRunTime(takeLong, 1)); // 757
console.log(getRunTime(takeLong, 2)); // 636
const memoizedTakeLong = memo(takeLong);
console.log(getRunTime(memoizedTakeLong, 1)); // 676
console.log(getRunTime(memoizedTakeLong, 1)); // 0
console.log(getRunTime(memoizedTakeLong, 2)); // 6442.2) Try to memoize a function from your standard library that you normally use to produce random numbers. Does it work?
No, because random() function is not pure. Memoization would cause the memoized random function to return same value as when it was called for first time.
2.3) Most random number generators can be initialized with a seed. Implement a function that takes a seed, calls the random number generator with that seed, and returns the result. Memoize that function. Does it work?
// 32-bit random number generator getter
function getRandomGenerator(seed: number) {
let x = seed;
let a = 69069;
let c = 1;
return function random() {
x = (x * a + c) % Math.pow(2, 32);
return x;
}
}
const random = getRandomGenerator(100);
console.log(random()); // 6906901
console.log(random()); // 311375314
console.log(random()); // 1480311595
console.log(random()); // 1945073776
function runWithSeed(seed: number) {
const random = getRandomGenerator(seed);
return random();
}
console.log(runWithSeed(100)); // 6906901
console.log(runWithSeed(100)); // 6906901
console.log(runWithSeed(100)); // 6906901
console.log(runWithSeed(100)); // 6906901Code snippet above demonstrates solution for this challenge using one of the most simple random number generators – linear congruent generator.
If result of random() call would depend on something outside getRandomGenerator scope (such as time etc.), it wouldn’t be possible to memoize runWithSeed function.
2.4) Which of these C++ functions are pure? Try to memoize them and observe what happens when you call them multiple times: memoized and not.
- Factorial – pure
- std::getchar() – impure (depends on stdin)
- f() – is impure – memoizing would cause print to stdout only on first call
- f(int x) – is impure – result depends on static int y;, which is stored outside of scope and updated each call
2.5) How many different functions are there from Bool to Bool? Can you implement them all?
Four.
| fx | fx(true) | fx(false) | Definition | Funcition name |
|---|---|---|---|---|
| f1 | true | true | f1(x) = true | T |
| f2 | true | false | f2(x) = x | identity |
| f3 | false | true | f3(x) = ¬x | negation |
| f4 | false | false | f4(x) = false | F |
2.6) Draw a picture of a category whose only objects are the types Void, () (unit), and Bool; with arrows corresponding to all possible functions between these types. Label the arrows with the names of the functions.
| To Void | To Unit | To Bool | |
| From Void | identity: Void -> Void | absurd: Void -> () | absurd: Void -> Bool |
| From Unit | – | identity: Unit -> Unit | fx: Unit -> Bool (f1() = true, f2() = false) |
| From Bool | – | unit: Bool -> () (unit (x) = ()) | identity: Bool -> Bool (T(x)=true, id(x)=x, neg(x)=¬x, F(x)=false) |